波形観測からスタートしたオシロスコープにはデジタル化によりさまざまな機能が搭載されました。
特に波形から多くの情報を自動的に引き出す能力はデジタル演算能力の向上により大きく進化しました。
従来、波形データを外部コンピューターに転送し、演算処理していたことは過去の遺物になったのかもしれません。とりわけ機能評価で多くの実験を行う場合には効率を飛躍的に高めることができます。
波形パラメータの定義
パルス波形の形状を数値として表すために波形パラメータが使われます。
図1のように振幅方向、時間方向に決められているため、これらの値からパルスの形状を定量的に規定することができます。半導体のAC特性でおなじみです。
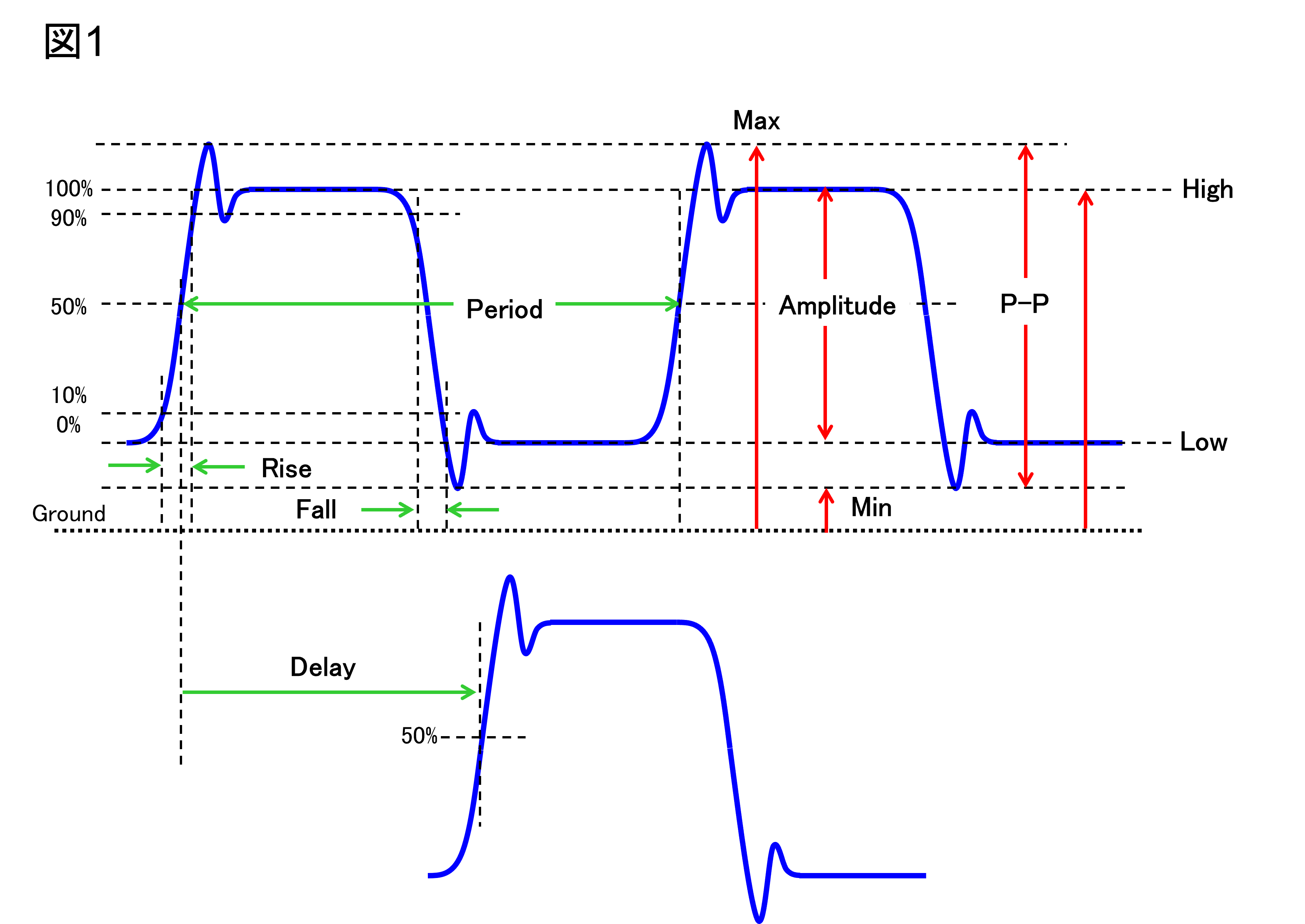
図1 波形パラメータの定義
図2は横河計測のオシロスコープDLM3054での自動パラメータ測定のメニューです。
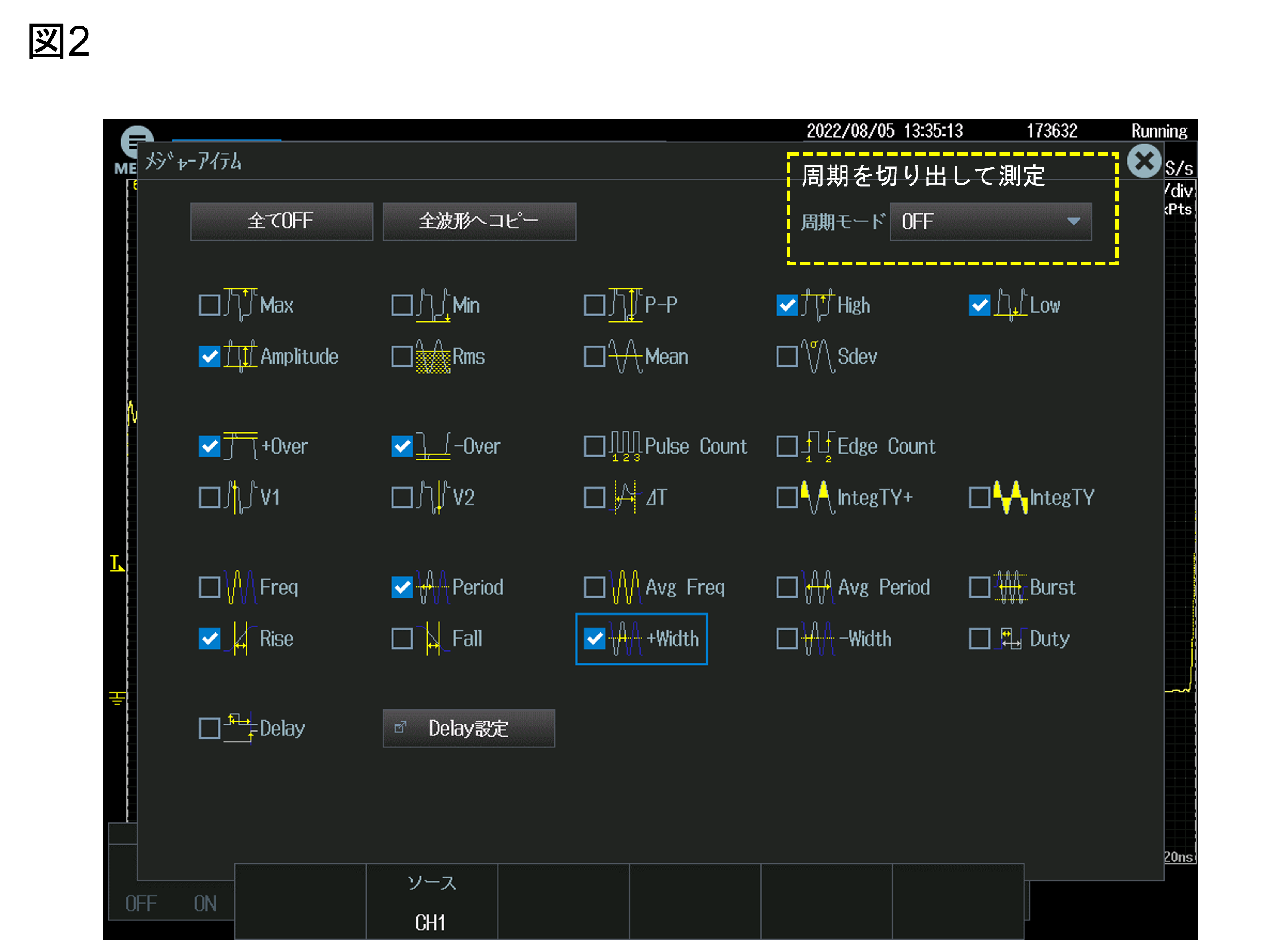
図3はパルス波形での各種パラメータの測定結果です。
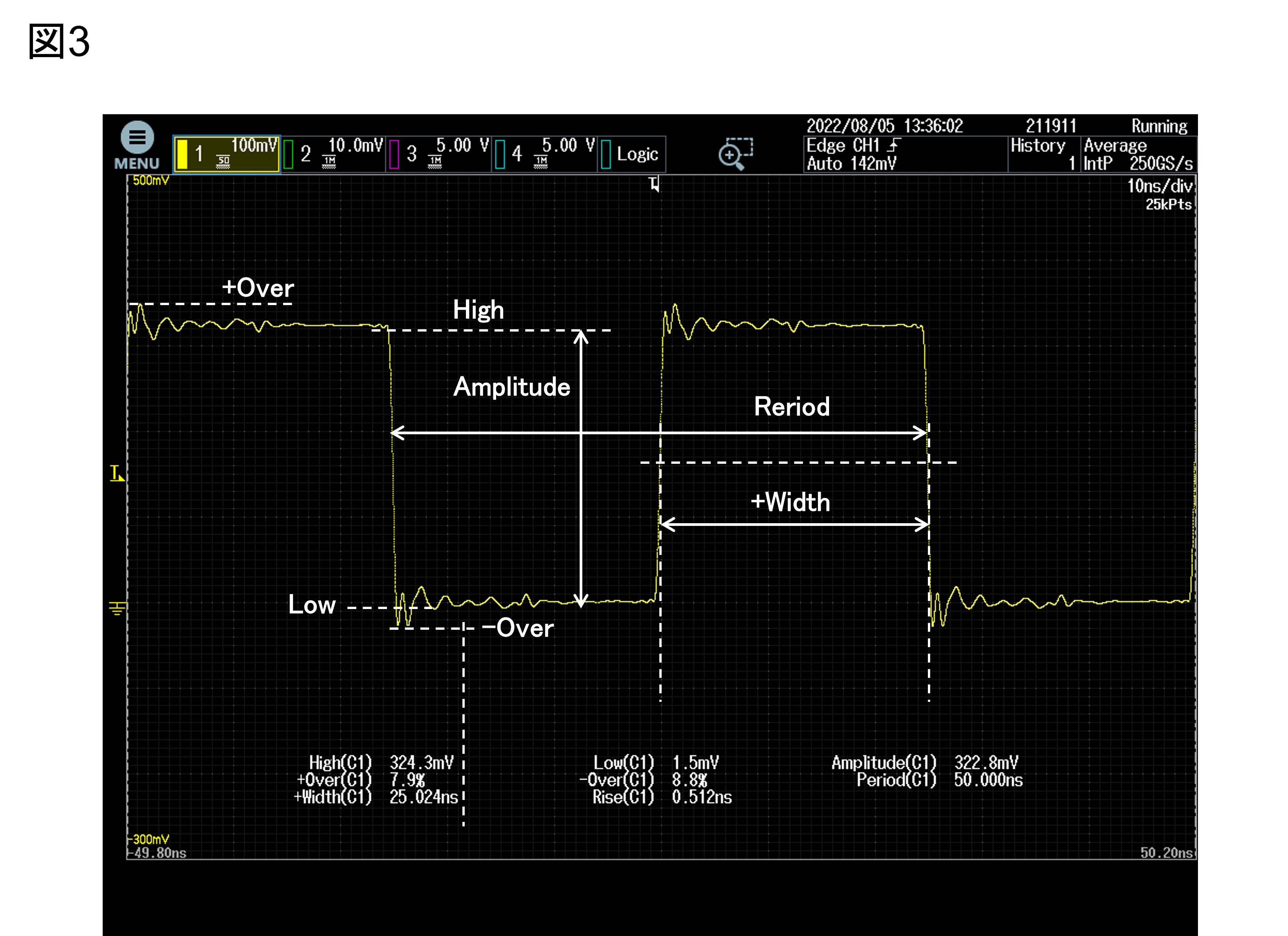
図3 波形パラメータの測定結果
波形パラメータ測定基本原理
波形パラメータの測定原理は図4のようになります。
初めに基準となるLowレベル、Highレベルを密度から求めます。これから振幅の10%、50%、90%の値が分かります。これらの電圧に相当する時間を補完により算出することで立上り/立下り時間、周波数(周期)パルス幅、デューティ比などが求まります。
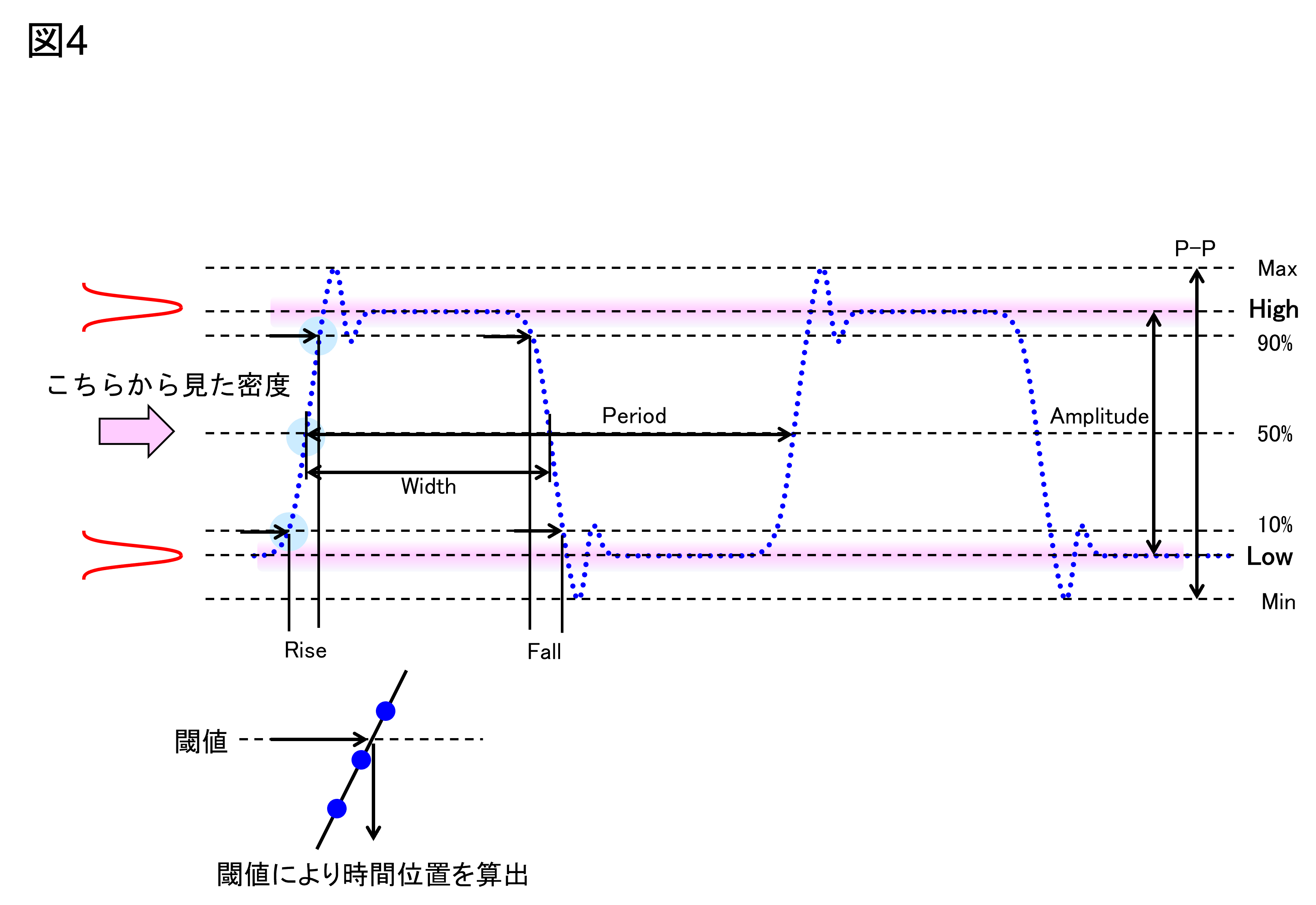
図4 波形パラメータの測定原理
横河計測のオシロスコープDLM3054の場合自動パラメータ測定のメニューの右上に「周期を切り出して測定」というタブがあります。
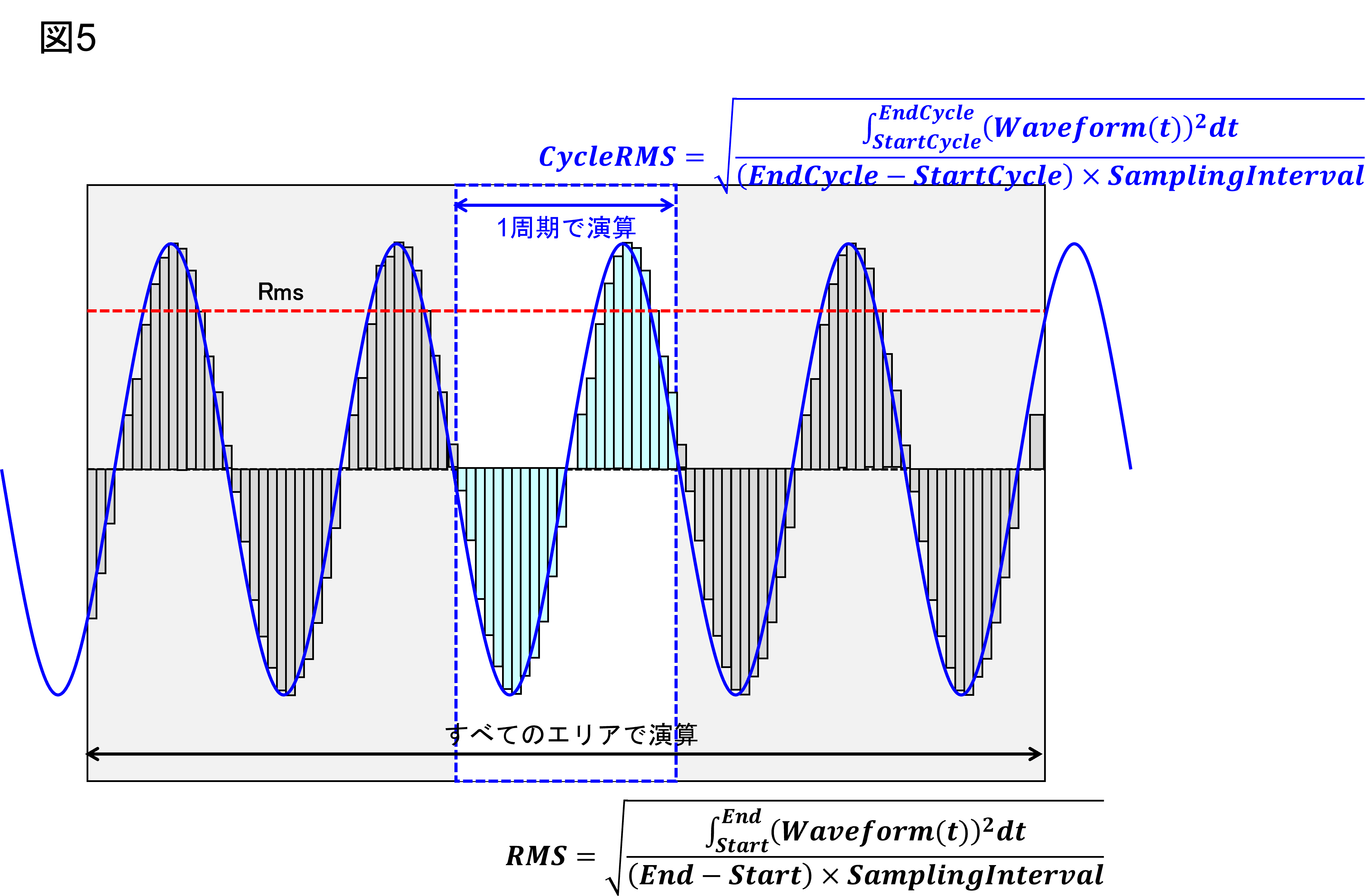
実効値、平均値等の算出では周期で正規化しなければなりません。
通常、演算はメモリ全体で行われます。しかし図5のように周期(の整数倍)がメモリサイズと一致するケースは稀でしょう。そのために1周期ないし周期の整数倍のデータ範囲で計算する指定が「周期を切り出して測定」です。
計測結果の確認にはカーソルによるマニュアル測定も有効
便利なパラメータ演算ですが、波形歪が大きい場合には予想した結果と異なる値になることがあります。
そのため場合によってはカーソルによる測定も併用しましょう。
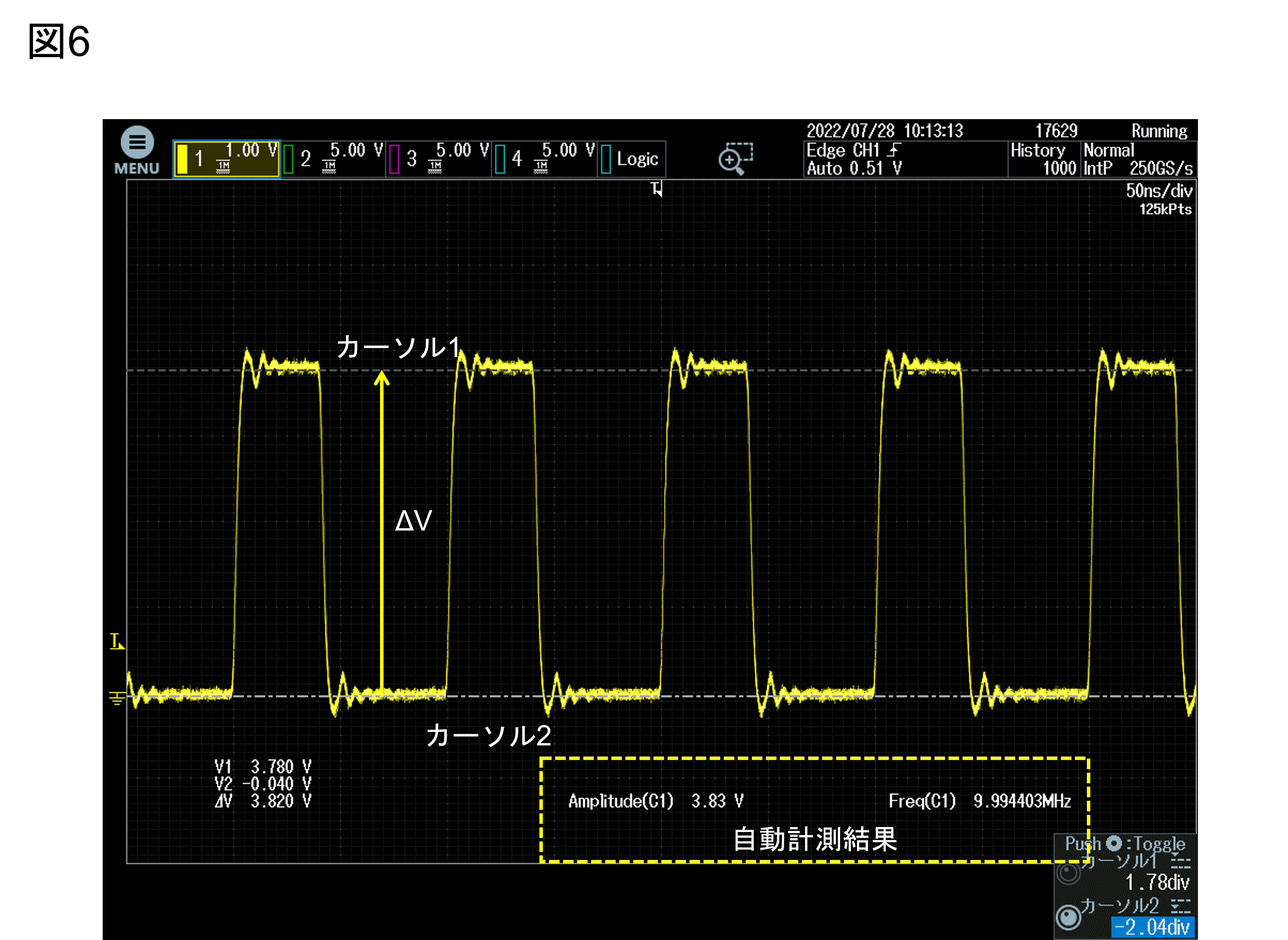
図6 カーソルによる測定
遅延時間測定の統計解析
自動パラメータの測定では任意の時間間隔を測定できます。
図7はCH1の立上りエッジを基準にCH2の立上りエッジまでの時間を測定する例です。
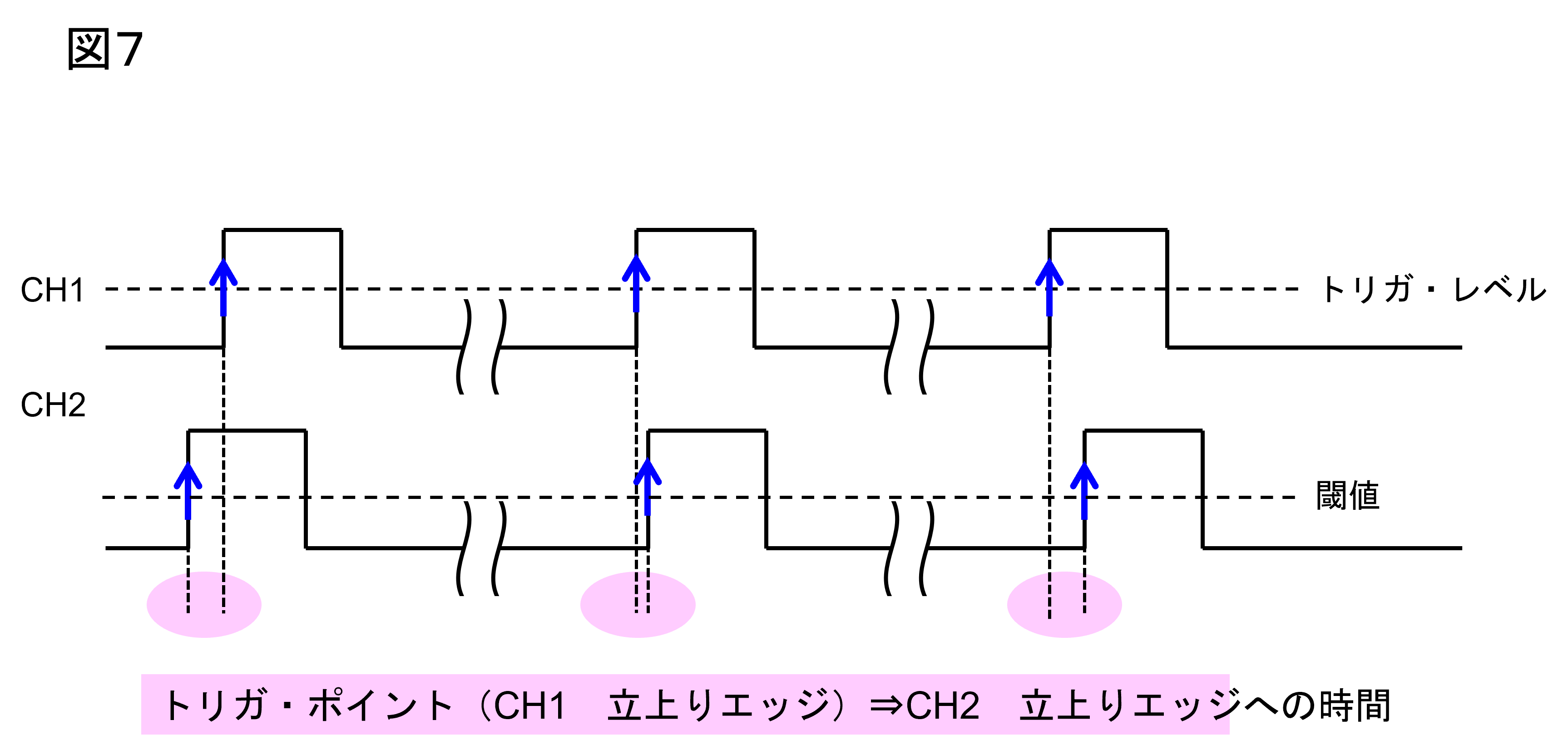
図7 変化するエッジ間時間
図8は残光時間100msにて変化する様子を確認した例です。変動のイメージは分かりますが定量的には分かりません。
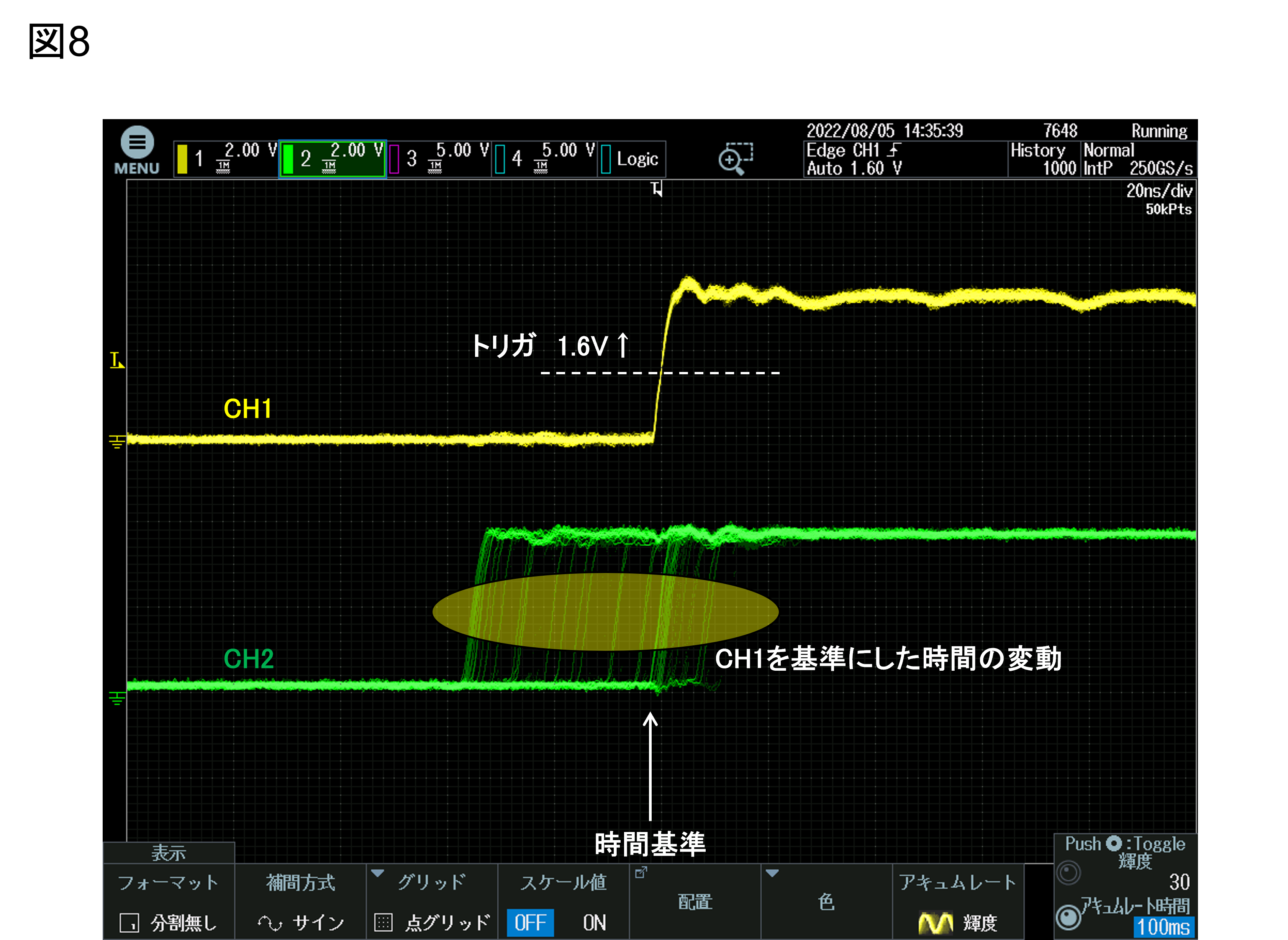
図8 残光時間可変モードにて変化の様子を観測
そこで蓄積時間を無限大に設定した結果が図9です。
振れの最大が分かります。色により大体の分布イメージは分かります。
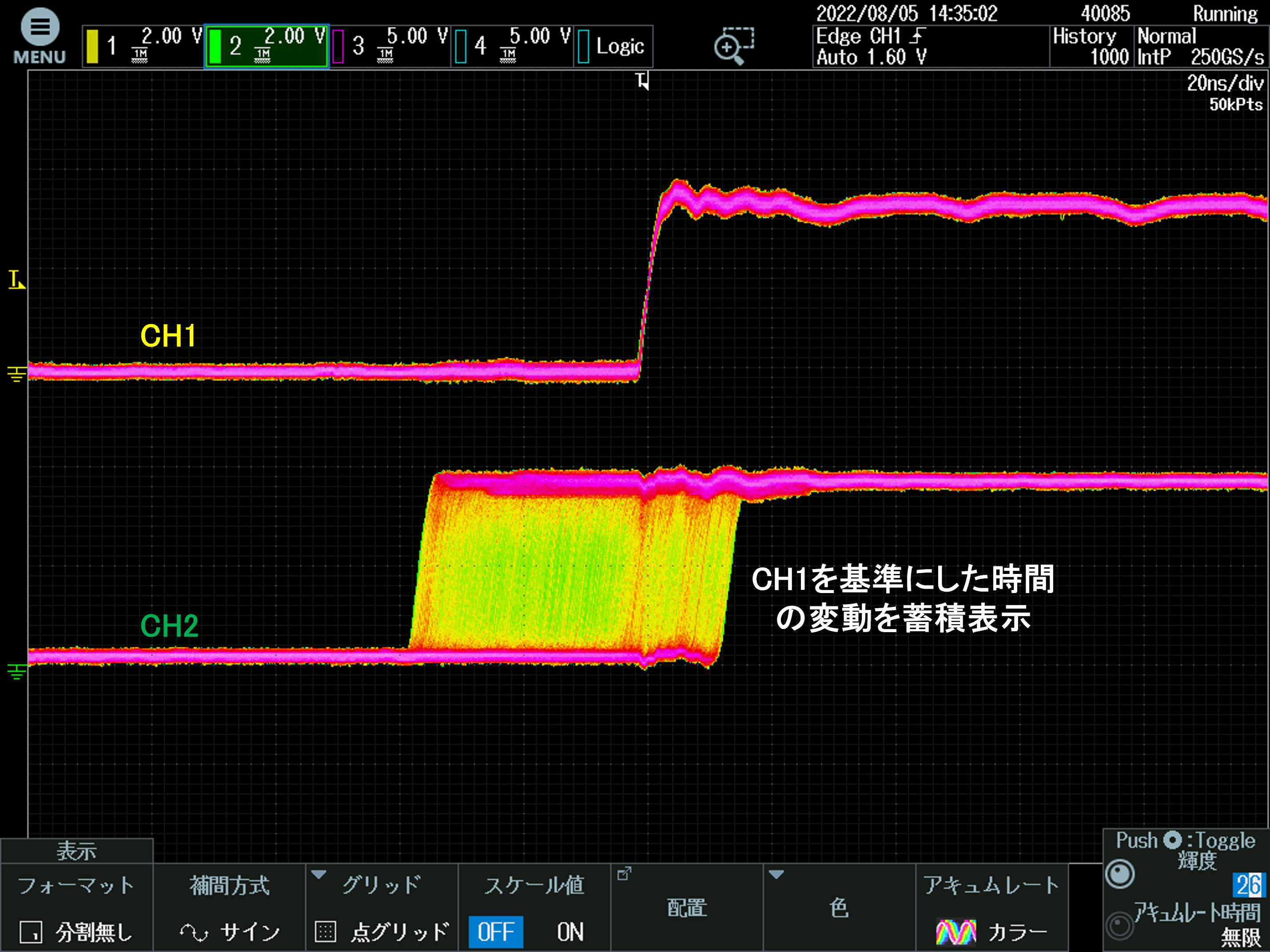
図9 残光時間無限大にて変化のピークを観測
図10は721回取り込み、取り込みごとにエッジ間の時間を測定し、時間ずれの頻度を解析した例です。
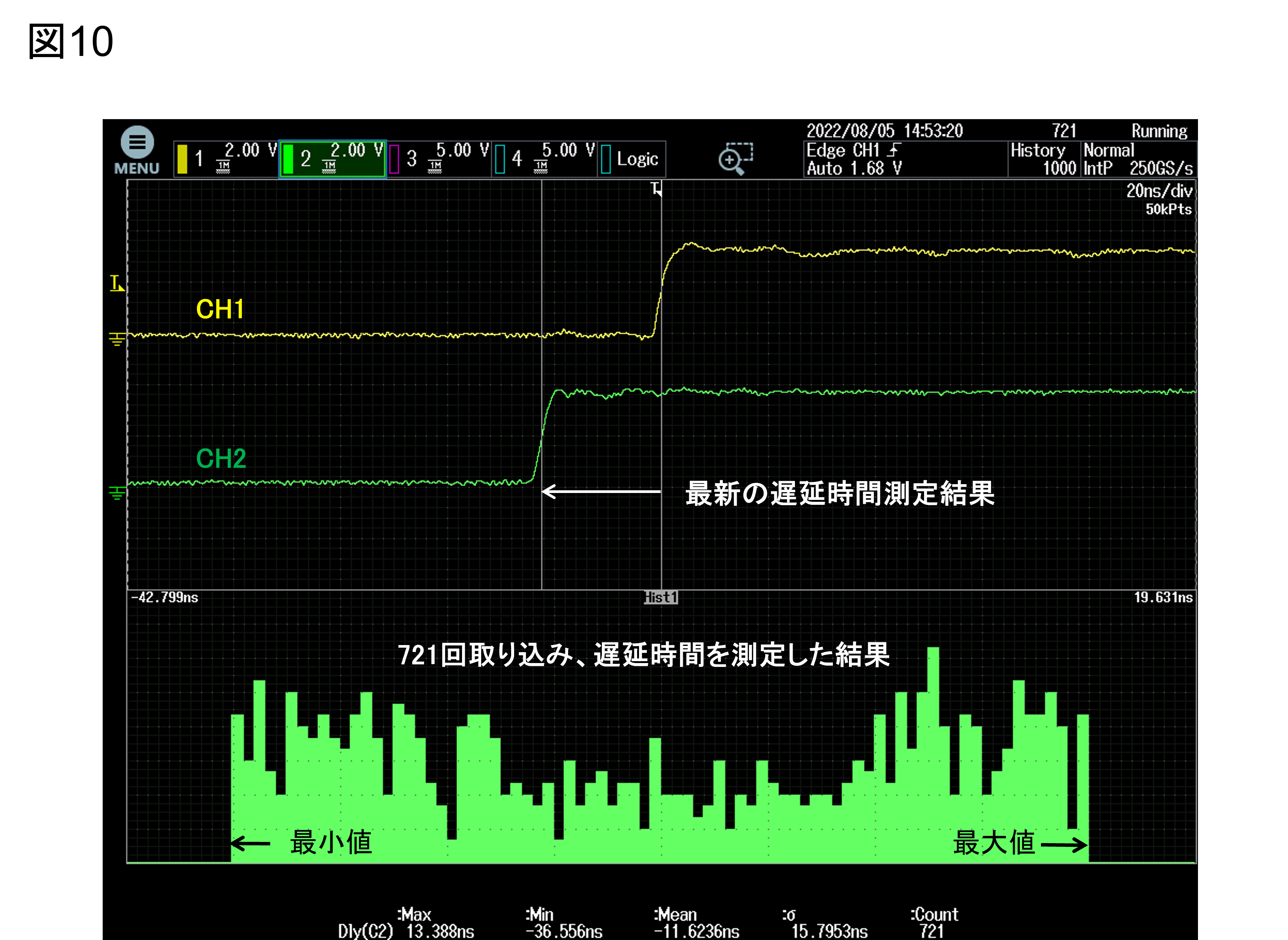
図10 時間ずれの統計解析
オシロスコープによる波形パラメータ演算は演算処理に演算パワーが取られるために波形取り込みレートは低下する傾向があります。この点には注意しましょう。
システムの応答時間のばらつきを調べる
図11はシステムのスタートパルスの立下り以降にI2Cにアドレス18Hが発生する例です。
ここでは
CH1 I2C SCLK(シリアルクロック)
CH2 I2C SDAT(シリアルデータ)
CH3 スタート信号
拡張トリガ I2C
トリガ・モード ノーマル
になります。
遅延時間測定にてトリガ・ポイント(アドレス18H)を基準にスタートパルスの立下りエッジまでの時間を求めます。
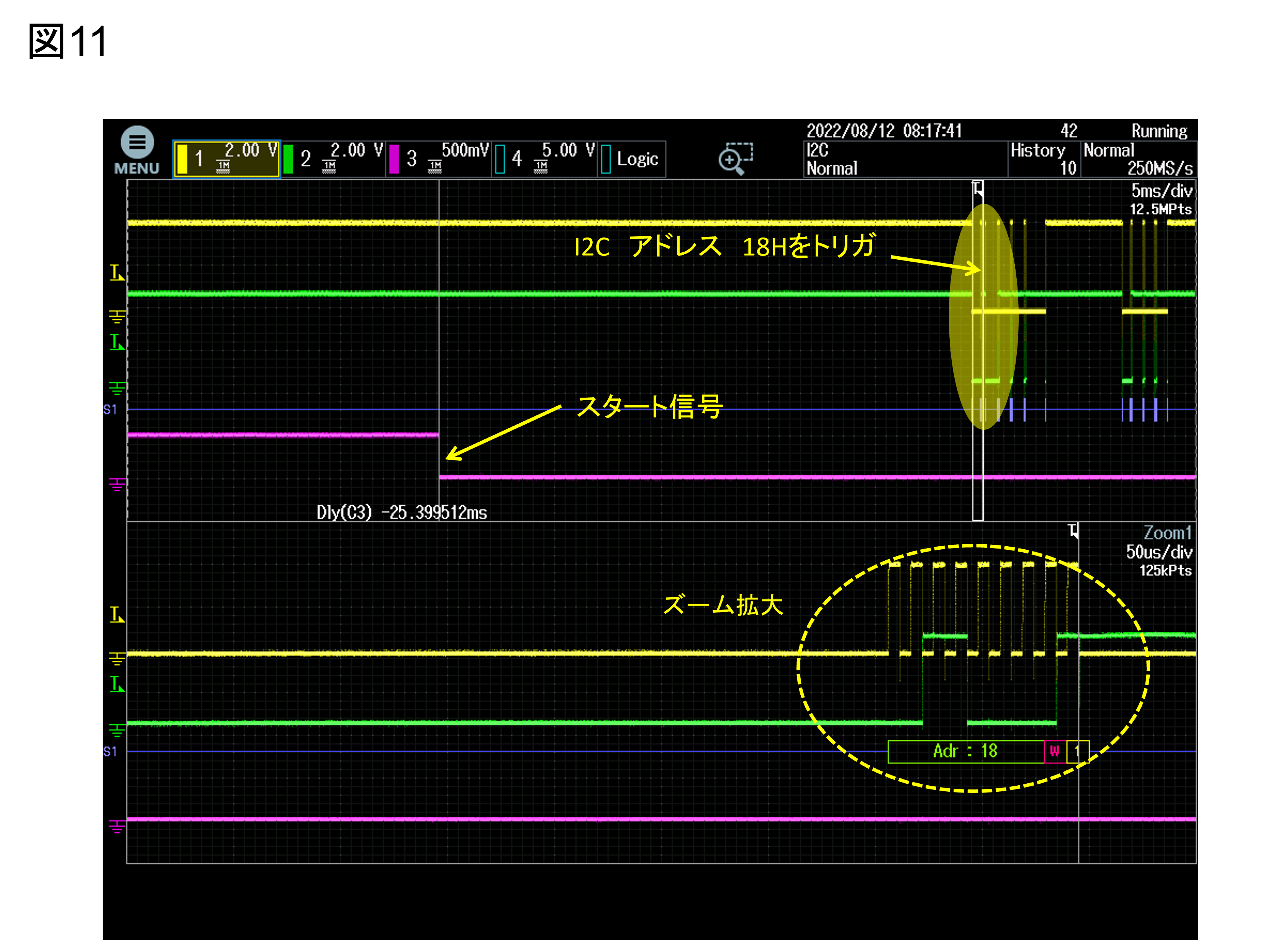
図11 I2Cの指定アドレスが出力されるまでの時間を測定
図12は100回スタートを繰り返し、遅延時間のばらつきを観測した例です。
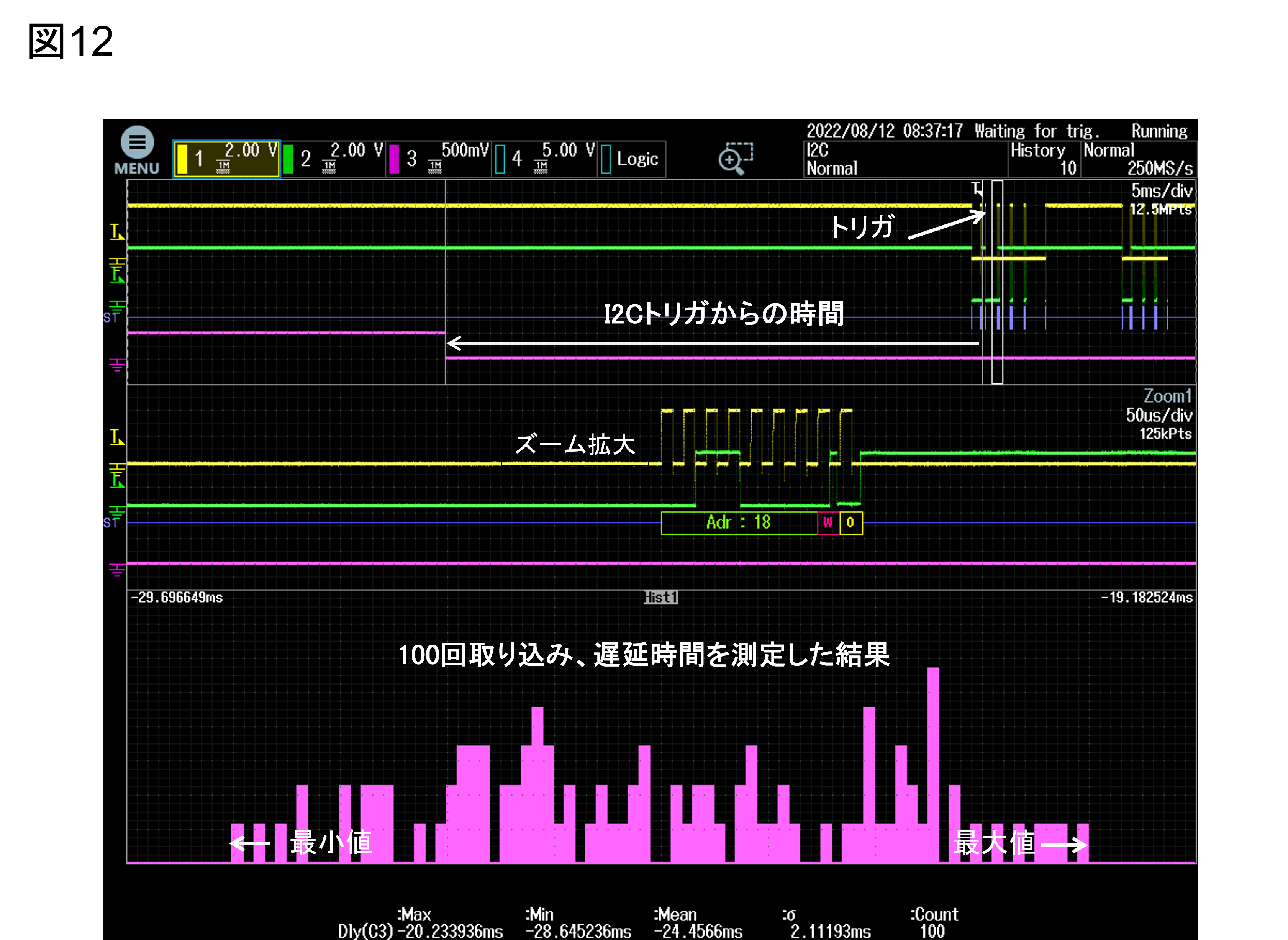
図12 応答時間のばらつきを統計解析
オシロスコープのみで100回の実験統計解析を行えます。
このような手法で実験時間、解析時間を大幅に低減できます。