電気に関係のない世界でもデシベルという言葉を耳にします。
例えば、騒音を数値化する場合にデシベルが使われます。
図1は人間の感じる音のレベルと音圧の関係です。
音圧は圧力なのでPa(パスカル)が単位になりますが、20μPaから2千万μPaまで100万倍の差があります。
そのためリニアに表現するのではなく対数を使う、10倍ごとに20dB増加するデシベル評価が一般に使われます。
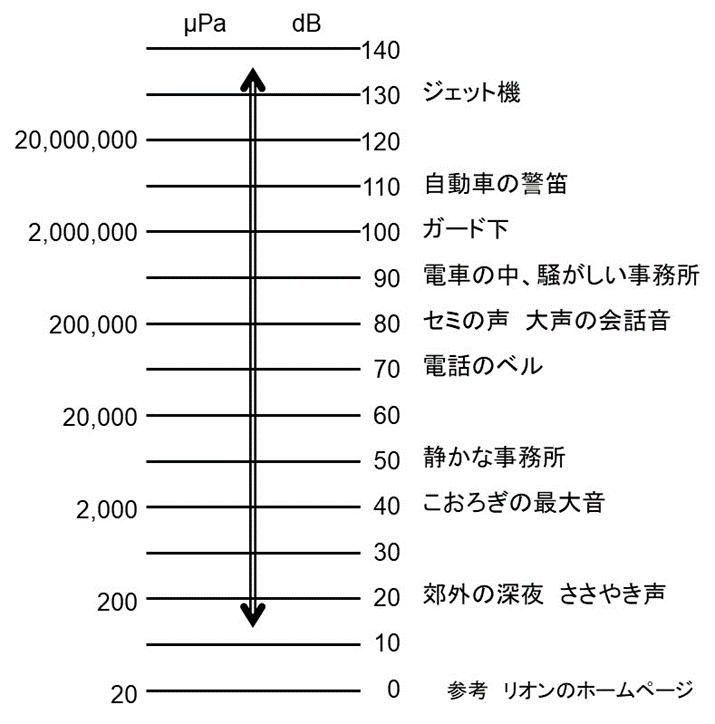
図1 音圧と音圧レベルの関係 (リオン株式会社のホームページhttps://svmeas.rion.co.jp/support/st_sound.htmlから作成)
図2は騒音計の例です。
この製品では人間が聴覚可能な範囲の周波数に重み付けをするA特性にて25~138dBのレベルを測定でき、人間の聴力範囲をカバーしています。

図2 騒音計の例
レコーダ、オシロスコープなどの波形を観測する計測器では、ダイナミック・レンジがあまり広くないこともあり、対数表示は使われません。
図3は振幅1と0.001のサイン波を同時に表示した例です。
振幅に1000倍の差があるため振幅0.001のサイン波の形状を確認することはできません。
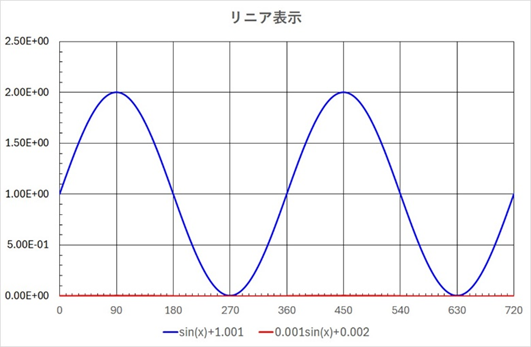
図3 リニア表示で振幅差の大きな信号を表示した場合
図4は同じ条件で縦軸を対数表示に変更した例です。
縦軸は1目盛り毎に10倍になるため振幅0.001のサイン波は確認できますが、逆に振幅1のサイン波は形状が大きく変形しています。
波形表示では表示歪は許されませんから対数表示は不向きです。
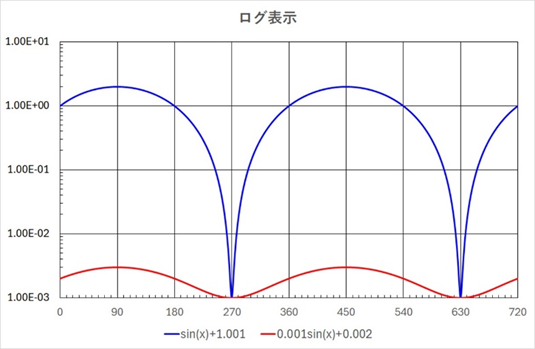
図4 対数表示で振幅差の大きな信号を表示した場合
図5は振幅に100倍に差がある1kHzと10kHzが重畳した信号の時間軸表示(縦軸 リニア)と周波数軸表示(縦軸 対数)の例です。
左側の時間軸表示では10kHzの信号の存在は分かりません。
しかし、右側の周波数軸表示では10kHzの成分が確認できます。
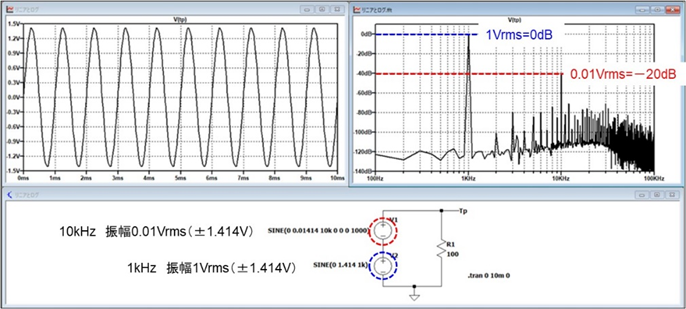
図5 周波数軸表示で対数表示は有効
ここでは図6のように縦軸は-140dB~0dB(上に若干の余裕)と1000万倍のレンジを、また横軸も対数表示で100Hz~100kHzまで1千倍のレンジを表示しています。
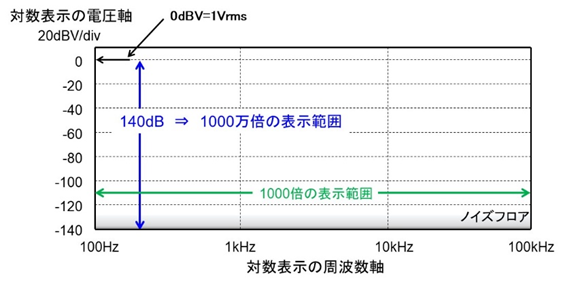
図6 縦軸・横軸ともに対数表示
このように広い範囲を扱えるデシベルですが、図7のように電圧・電流と電力では計算が異なります。
電圧・電流では10倍毎に20dB、電力では10dBになります。
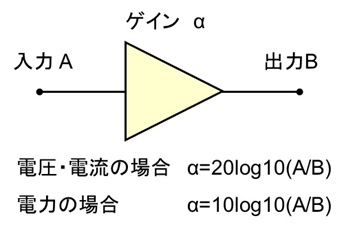
図7 デシベルの計算式
デシベルは比が1以下の場合はマイナスの値になります。
図8はリニアの比率とデシベルの関係を示しており、1/100万分~100万を-120~+120dBで表示しています。
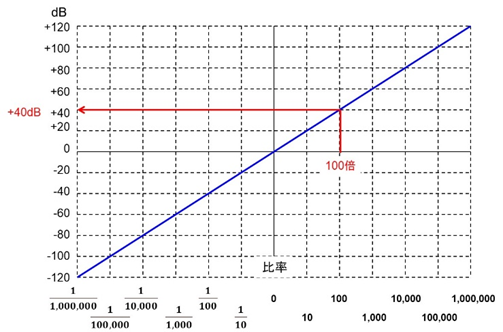
図8 比率とデシベル
さて、なぜ電力では10倍毎に10dBなのでしょうか。
図9のように電力は電圧と電流の掛け算になり、電圧が10倍になると電流も10倍になり、電力は100倍になります。
このため電力では計算が変わってきます。
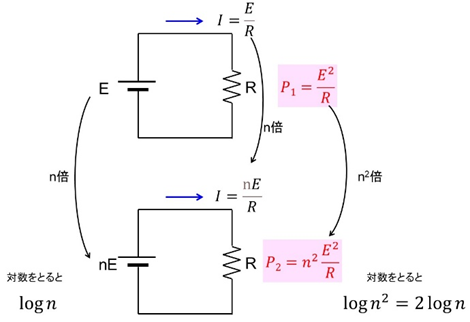
図9 電圧・電流と電力でデシベル計算は異なる
デシベル表示ではもう一つ便利なことがあります。
図10のように100倍、0.5倍、10倍の増幅系の場合、リニアの計算ではすべてをかけることになります。
対数の掛け算は足し算に、割り算は引き算になるため、対数の計算では40-6+20=54dBと簡単に行えます。
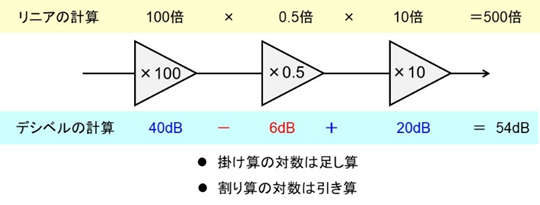
図10 ゲイン計算が楽になるデシベル
デシベル表示が使われる例としてA/D変換器のビット数と分解能の関係があります。
A/D変換器では1ビットあたり2倍の差(6dB)があるためダイナミック・レンジは次のようになります。
8ビット A/D 48dB
12ビット A/D 72dB
16ビット A/D 96dB
24ビット A/D 144dB
1ビットが2倍になるので6dB相当とすると覚えやすくなります。
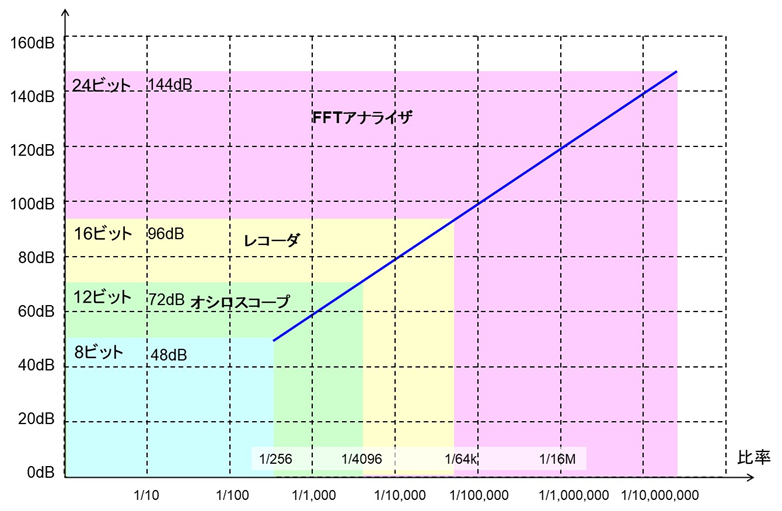
図11 計測器で異なるビット数とデシベルの関係
デシベルは単位のない比率だけでなく、絶対値の場合もあります。
l dBm・・・スペクトラム・アナライザなどで高周波の電力を表す0dBm=1mW (50Ω系)
l dBV・・・音響機器の入出力のレベルの表記などに用いられる電圧を表す 0dBV=1V
l dBv・・・600Ω系にて1mWの電力に相当する電圧 0dBv=0.775V
などがあります。